지난 포스팅에서는 VaR을 측정하는 방법 중 하나인 Time Series Approach에 대해 알아보았다.
이번 포스팅부터는 RiskMetrics와 Time Series Approach보다 좀더 세련(?)된 VaR 측정 방법에 대해 알아보려고 한다.
이를 위해서 우선 Extreme Value Theory에 대해 알아보아야 하는데 이번 포스팅에서는 이에 대해 소개하려고 한다.
금융 시장에선 리스크 관리란 큰 손실로부터 투자자를 보호하는 것이기 때문에 극단적인 손실과 같이 잘 일어나지 않을 사건들을 이해하는 것이 중요하다.
극단값이론(Extreme Value Theory, EVT)은 이러한 극단적인 손실의 발생에 관점을 맞추어 VaR 계산하는 방법을 제공한다.
지금부터 EVT가 무엇인지 간단하게 알아보자.
| Def 15.1 표본 $x_1, \cdots, x_T$의 순서통계량은 다음과 같은 오름차순으로 정렬했을 때 특정 순서에 있는 값들을 의미한다. $$ x_{(1)} \le x_{(2)} \le \cdots \le x_{(T)}.$$ 이때 $x_{(i)}$를 $i$번째 순서통계량이라고 하고, $x_{(1)}$와 $x_{(T)}$는 각각 표본최솟값, 표본최댓값을 의미한다. |
| Def 15.2 확률변수 $X$가 $P(X=c)=1$이면 $c$에서 퇴화(degenerate)된다고 한다. |
$\{ x_1, \cdots, x_T \}$로 표현되는 $\$$1에 대한 손실의 모음을 생각해보자.
우리는 $x_1, \cdots, x_T$가 누적분포함수 $F(x)$를 갖는 $iid$이고, 그 값의 범위는 $[l,u]$로 설정된다고 가정한다.
그러면 표본최댓값 $x_{(T)}$의 누적분포함수는 다음과 같다.

만약 $T \rightarrow \infty$일 때 $x <u$여서 $0<F(x)<1$이라면 $[F(x)]^T \rightarrow 0$이고, $x=u$여서 $F(x)=1$이라면 $[F(x)]^T \rightarrow 1$이다.
즉 다르게 말하면 최대손실 $x_{(T)}$의 분포가 표본의 크기 $T$가 커질수록 $u$에서 퇴화된다고 할 수 있다.
따라서 이러한 접근은 실제 최대 손실에 대해 잘 설명하지 못한다.
퇴화 문제를 해결하기 위해 위치모수(location parameter) $\mu$와 척도모수(scale parameter)가 있다고 가정하고 다음과 같이 정규화하면
$$x_{(T)}^* = \frac{x_{(T)} - \mu}{\sigma}$$
이는 Generalized Extreme Value(GEV) 분포를 따른다.
GEV 분포의 정확한 정의는 다음과 같다.
확률변수 $x$에 대해 $x^*$는 $x^* = (x - \mu)/ \sigma$로 정규화된 값이라고 할때, $x^*$에 대한 GEV의 누적분포함수는 다음과 같이 정의된다.

$\text{where}~\xi$는 척도모수.
이제 미분적분학 제1정리를 이용해 GEV 분포의 확률밀도함수를 다음과 같이 구할 수 있다.
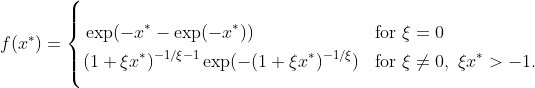
우리는 정규화된 최대손실 $x_{(T)}^* = (x_{(T)} - \mu) / \sigma$가 GEV 분포를 따른다고 가정했고 이는 3개의 모수 ― 형상모수 $\xi$, 위치모수 $\mu$, 척도모수 $\sigma$ ―를 포함한다.
이제 우리가 해야할 일은 이 3가지 모수를 추정하는 일이고, 곧 이 일이 VaR를 측정하는 방법으로 이어진다.
오늘은 또다른 VaR을 구하는 방법을 알기전 준비 단계인 EVT에 대해 간단하게 알아보았다.
다음 포스팅에서는 위에서 말한 3가지 모수를 추정하는 방법 중 하나인 Block Maxima에 대해 알아볼 예정이다.
오늘은 여기까지.
'FinancialTimeSeries' 카테고리의 다른 글
| 17. Value at Risk(7) (0) | 2024.07.28 |
|---|---|
| 16. Value at Risk(6) (3) | 2024.07.22 |
| 14. Value at Risk(4) (1) | 2024.07.08 |
| 13. Value at Risk(3) (0) | 2024.07.01 |
| 12. Value at Risk(2) (0) | 2024.05.27 |

