지난 시간에는 서로 다른 분산을 가지는 이분산성 시계열 모델을 다루는 가장 기본적인 모델인 ARCH 모델에 대해 알아보았다.
오늘인 ARCH 모델 이외에 또 다른 이분산성 모델에 대해 알아보려고 한다.
| Def 10.1. Generalized Autoregressive Conditional Heteroskedasticity(GARCH) 모델은 $\sigma_t^2 = f(I_{t-1})$을 다음과 같이 정의하고 GARCH($m,n$)이라고 한다. $$ \sigma_t^2 = a_0 + \sum_{i=1}^m a_i \varepsilon_{t-i}^2 + \sum_{j=1}^n b_j \sigma_{t-j}^2,$$ $\text{where}~a>0,~a_i \ge 0,~b_j \ge 0,~\text{and}~\sum_{i=1}^{max(m,n)}(a_i + b_i) <1.$ |
일반적으로 ARCH($m$) 모델에서 lag 값 $m$은 큰 값을 필요로 하기 때문에 추정해야 하는 모수들도 그만큼 늘어난다.
반면 GARCH 모델을 사용할 땐 GARCH(1,1) 모델만으로 금융 시계열에 적합하기 때문에 좀 더 유용한 측면이 존재한다.
다음과 같은 GARCH(1,1) 예시를 살펴보자.
$$ \sigma_t^2 = a_0 + a_1 \varepsilon_{t-1}^2 + b_1 \sigma_{t-1}^2, \tag{1}$$
$\text{where}~a>0,~a_1 \ge 0,~b_1 \ge 0,~\text{and}~a_1 + b_1 <1.$
이때 $\eta_t = \varepsilon_t^2 - \sigma_t^2$으로 정의하고 매우 작다고 가정해보자.
그러면 식 (1)을 다음과 같이 다시 쓸 수 있다.

위의 식을 통해 알수 있는 점은 충격의 제곱값인 $\varepsilon_t^2$값을 근사적으로 ARMA(1,1) 모델로 표현할 수 있다는 것이다.
대부분의 GARCH 모델의 계수 $b_1$은 0.9로 표현된다.
이제 식 (1)의 GARCH(1,1) 모델을 이용해 변동성 예측을 해보자.

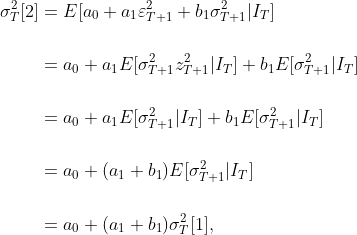
$$\vdots$$
다음을 특수한 GARCH 모델을 살펴보자.
| Def 10.2. Integrated GARCH(1,1) 모델은 $\sigma_t^2 = f(I_{t-1})$을 다음과 같이 정의하고 IGARCH(1,1)이라고 한다. $$ \sigma_t^2 = a_ 0 + a_1 \varepsilon_{t-1}^2 + (1- a_1) \sigma_{t-1}^2,$$ $\text{where}~a_1+b_1=1.$ |
간단하게 $a_0=0$이라고 가정하면 다음과 같이 쓸 수 있다.
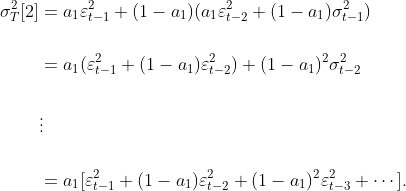
위 식을 통해 $a_1$이 0에 가까울수록 $\varepsilon_{t-1}^2, \varepsilon_{t-2}^2, \cdots$의 영향이 크고, $a_1$이 1에 가까울수록 $\varepsilon_{t-1}^2$의 영향이 크다는 것을 알 수 있다.
우리가 저번 포스팅에서 이야기 했던 수익률 데이터의 특징 중 하나가 바로 'leverage effect'였다.
leverage effect란 나쁜 정보가 좋은 정보보다 더 큰 영향을 끼친다는 현상을 의미한다.
지금부턴 이 leverage effect를 설명하는 이분산성 모델에 대해 알아보려고 한다.
| Def 10.3. Exponential GARCH 모델은 $\sigma_t^2 = f(I_{t-1})$을 다음과 같이 특정하고 EGARCH(m,n)이라고 한다. $$h_t = a_0 + \sum_{i=1}^m (a_i z_{t-i} + \gamma_i(|z_{t-i}| - E[|z_{t-i}|]))+ \sum_{j=1}^n b_j h_{t-j},$$ $\text{where}~h_t = \ln \sigma_t^2.$ |
EGARCH 모델이 어떻게 leverage effect를 설명하는지 알아보기 위해 간단하게 다음과 같은 꼴의 EGARCH(1,1) 모델을 살펴보자.
$$h_t = a_0 + a_1 z_{t-1} + \gamma_1 (|z_{t-1}| - E[|z_{t-1}|])+ b_1 h_{t-1}. \tag{2}$$
$h_t - b_1 h_{t-1} = \ln (\sigma_t^2 / \sigma_{t-1}^{2b_1})$임과 표준정규분포 $z_t$에 대하여 $E[|z_t|] = \sqrt{2/\pi}$임을 이용하면 식 (2)를 다음과 같이 다시 쓸 수 있다.
$$ \ln \left( \frac{ \sigma_t^2 }{ \sigma_{t-1}^{2b_1} } \right) = a_0 + a_1 z_{t-1} + \gamma_1 \left( |z_{t-1}| - \sqrt{ \frac{2}{\pi} } \right) .$$
위 식을 다시 $\sigma_t^2$에 대한 식으로 정리하면,

$\text{where}~a_0^* = a_0 - \gamma_1 \sqrt{2/\pi}.$
$a_1$이라면 나쁜 정보가 더 큰 영향을 끼친다는 것을 알 수 있다.
leverage effect를 설명하는 모델을 하나 더 알아보고 이번 포스팅을 마무리하자.
| Def 10.4. Threshold GARCH 모델은 $\sigma_t^2 = f(I_{t-1})$을 다음과 같이 특정하고 TGARCH(m,n)이라고 한다. $$ \sigma_t^2 = a_0 + \sum_{i=1}^m (a_i \varepsilon_{t-1}^2 + \eta_i D_{t-i} \varepsilon_{t-i}^2) + \sum_{j=1}^n b_j \sigma_{t-j}^2,$$ $\text{where}~ D_{t-i}$ is the indicator equal to one for $\varepsilon_{t-i}<0$ and 0 otherwise. |
TGARCH(m,n) 모델에서 $\varepsilon_{t-i}$이 임계점(threshold)값으로 설정된 0보다 큰지 작은지에 따라 조건부 분산 $\sigma_t^2$에 주는 영향은 다르다.
예를 들어 TGARCH(1,1) 모델에 대해서 조건부 분산 $\sigma_t^2$을 다음과 같이 다시 쓸 수 있다.
$$\sigma_t^2 = a_ 0 + (a_1 + \eta_1 D_{t-1})\varepsilon_{t-1}^2 + b_1 \sigma_{t-1}^2.$$
좋은 정보($\varepsilon_{t-1} >0$)에 대해서 $\varepsilon_{t-1}^2$이 $\sigma_t^2$에 주는 영향은 $a_1 \varepsilon_{t-1}^2$이지만,
나쁜 정보($\varepsilon_{t-i}<0$)에 대해서 $\varepsilon_{t-1}^2$이 $\sigma_t^2$에 주는 영향은 $(a_1 + \eta_1) \varepsilon_{t-1}^2$이다.
위의 TGARCH 모델을 좀더 일반화한 모델은 다음과 같다.
| Def 10.5. Glosten, Jagannathan, and Runkle의 GARCH 모델은 $\sigma_t^2 = f(I_{t-1})$을 다음과 같이 특정하고 GJRGARCH(m,n)이라고 한다. $$ \sigma_t^2 = a_0 + \sum_{i=1}^m (a_i \varepsilon_{t-1}^2 + \eta_i D_{t-i} \varepsilon_{t-i}^2) + \sum_{j=1}^n b_j \sigma_{t-j}^2,$$ $\text{where}~ D_{t-i}$ is the indicator equal to one for $\varepsilon_{t-i}< \mu$ and 0 for $\varepsilon_{t-i} \ge \mu$. |
오늘은 지난 시간에 이어서 이분산성을 표현하는 모델에 대해서 알아보았다.
지금까지 배운 내용을 바탕으로 다음 포스팅부터 본격적으로 Financial Time Series 카테고리의 목표인 Value at Risk에 대해 다룰 예정이다.
오늘은 여기까지.
'FinancialTimeSeries' 카테고리의 다른 글
| 12. Value at Risk(2) (0) | 2024.05.27 |
|---|---|
| 11. Value at Risk(1) (0) | 2024.05.20 |
| 09. Conditional Heteroskedastic Model(1) (0) | 2024.04.29 |
| 08. Unit-Root Test & Seasonality (0) | 2024.04.01 |
| 07. ARIMA Model (0) | 2024.03.24 |



