겨울방학 시계열 프로젝트가 끝났다.
약 5주간의 시간이 주어졌지만 설연휴가 껴있어서 체감은 3주였다..
처음 시계열 프로젝트 조가 짜여지고 조원들과 주제를 선정하기 위해 이야기를 하다보니 시계열을 처음 접해본 조원들이 많다는 것을 알 수 있었다.
그래서 시계열을 처음 접해본 사람들이 어렵지 않게 할 수 있고 많은 것을 배울 수 있는 주제는 무엇이 있을지 생각해보다가, 최종적으로 다음과 같이 주제를 정했다.
VAR 모델을 이용한 포트폴리오의 수익률 예측과 Value at Risk 측정
VAR 모델을 설정하는 과정까지가 사실상 시계열의 기초이자 핵심인데 이러한 주제로 프로젝트를 진행한다면 시계열을 처음 접해본 입장에서 많은 것을 얻어 갈 수 있을 것이라고 생각했다.
이번 포스팅에서는 우리가 진행한 프로젝트의 발표 자료를 통해 복기하는 시간을 가져보려고 한다.
#Topic&Contents


발표 주제와 목차는 위와 같다.
#Goal&Timeline


우리 프로젝트의 가장 큰 목표는 시계열 모델을 경험하는 것이다.
그 중 VAR 모델은 사실 경제·금융 분야에서 가장 많이 사용 되지만 다른 분야에도 충분히 적용할 수 있다.
Timeline을 보게되면 우리 프로젝트의 큰 흐름을 알 수 있다.
이제 본격적인 프로젝트 내용을 알아보자.
#IntroductionToTimeSeries


기초적인 시계열에 대한 내용으로 발표를 시작하였다.
우리가 최종적으로 이용할 VAR 모델과 인과관계가 있는 변수가 없을 경우를 대비한 AR 모델에 대해 소개하였다.
두 모델은 이전 정보를 이용한다는 공통점이 있다.
하지만 가장 큰 차이점은 AR 모델은 자기 자신만의 정보만을 이용하고 VAR 모델은 다른 변수의 정보까지 이용한다는 것이다.
이러한 AR, VAR 모델을 만들기 위한 시계열 데이터는 '정상성'을 가정한다.

정상성이란 시계열 데이터의 평균과 분산은 시점에 상관없이 일정하고, 공분산은 시점이 아닌 시차에만 영향을 받는다는 의미이다.
이러한 정상성에 대한 가정은 AR, VAR 모델 뿐만 아니라 대부분의 시계열 모델에서 가정하고, 차분이나 로그 변환을 통해 정상성을 만족시킨다.
우리에게 주어진 시계열 데이터가 정상성을 만족하는지 확인하기 위해 대표적인 정상성 검정법인 ADF 검정과 PP 검정을 실시하였다.
두 검정 모두 데이터 특성에 따라 기각역이 달라지는 특성이 있어 우리는 두 검정 모두 귀무가설을 기각하는 데이터를 만들어 사용하였다.
이제 VAR 모델을 만들기 위한 인과관계가 있는 변수를 선택하는 방법을 알아보자.

그 방법은 바로 그랜저-인과관계 검정이다.
이를 통해 인과관계가 있는 변수만 선택할 수 있고, 검정을 위한 차수는 비교적 적은 데이터에서 유리한 BIC를 이용하였다.
이제 위의 방법들을 이용해 실제 분석을 실행해보자.
#Analysis

조원들이 각각 뽑은 종목은 위와 같다.
2013년 1월부터 2022년 12월의 월별 수익률 데이터를 이용하였고, 최종적으로 2023년 1월의 수익률을 예측하고 실제 수익률과 비교할 생각이다.





각 종목별로 수집한 변수는 위와 같다.
노란색 형광펜으로 칠한 변수들은 그랜저-인과관계 검정에서 종목의 수익률에 영향을 준다고 판단된 변수들을 의미한다.
이때 셀트리온 종목은 모든 변수들이 수익률에 영향을 주지 않는다는 결과가 나와 임의로 변수를 선택해 VAR 모델을 생성하였다.





VAR 모델링을 한 결과와 수익률 예측을 위해 선정한 모델은 위와 같다.

선택한 모델을 이용해 각 종목별 2013년 1월 수익률의 예측값과 실젯값은 위와 같다.
아쉽게도 적지 않은 차이가 발생한다는 것을 알 수 있다.
이제 포트폴리오를 구성하기 위한 종목별 가중치를 구해보도록 하자.
#ValueatRisk


금융 시장에서 위험은 크게 시장 위험, 운영 위험, 신용 위험이 있다.
우리가 측정할 Value at Risk(VaR)는 대부분의 위험에 적용될 수 있지만 주로 시장 위험을 측정하는 지표로 사용된다.
VaR을 측정하는 방법은 다양하지만 대표적으로 RiskMetrics, TimeSeries Approach, Block Maxima, Peaks Over Threshold 등이 있다.
우리는 RiskMetrics를 이용하여 VaR을 측정할 것이다.


RiskMetrics는 J.P. Morgan에서 개발한 방법으로 1989년에 개발되어 회사 내부 보고용으로만 사용하다가 1992년에 고객들의 건의로 공개되었다고 한다.
자세한 방법은 위 자료를 참고하면 되고, RiskMetrics를 비롯한 VaR 측정 방법들에 대해 자세히 포스팅할 예정이다.

최종적으로 측정된 종목별 VaR는 위와 같다.
해석하는 방법은, 셀트리온을 예로 들면, 셀트리온에 1원을 투자했을 때 99%의 확률로 손실은 0.3533원보다 낮게된다는 것이다.
만약 KCC에 1억을 투자했을 경우 99%의 확률로 손실은 2966만원보다 낮게 된다.
이제 종목별 VaR를 구했으니 최종 포트폴리오의 VaR를 구할 차례이다.

포트폴리오의 VaR는 위와 같은데, 언뜻 복잡해보이지만 두번째 줄과 같이 행렬의 곱으로 쉽게 표현할 수 있다.
첫 번째 식에서 $ w_ i$는 $i$번째 종목의 가중치, $\text{VaR}_{i,1-p}$는 $i$번째 종목의 유의수준 $(1-p)$에 대한 VaR, $\rho_{ij}$는 $i$번째 종목과 $j$번째 종목의 상관계수를 의미한다.
포트폴리오의 VaR를 구하기 위해 우리는 상관계수와 가중치를 마저 계산해야 한다.

종목별 상관계수는 우리가 가지고 있는 수익률 데이터를 이용해 위와 같이 쉽게 계산할 수 있다.
이제 가중치를 구해보자.

가중치를 구하기 위한 조건은 다음과 같다.
첫째, 모든 가중치의 합은 1일 것.
둘째, 각 가중치의 최솟값은 0.05, 최댓값은 0.4일 것.
셋째, 첫째와 둘째 조건을 만족하면서 포트폴리오의 VaR를 최소화 할 것.
그 결과 각 종목별 투자 가중치는 위와 같다.
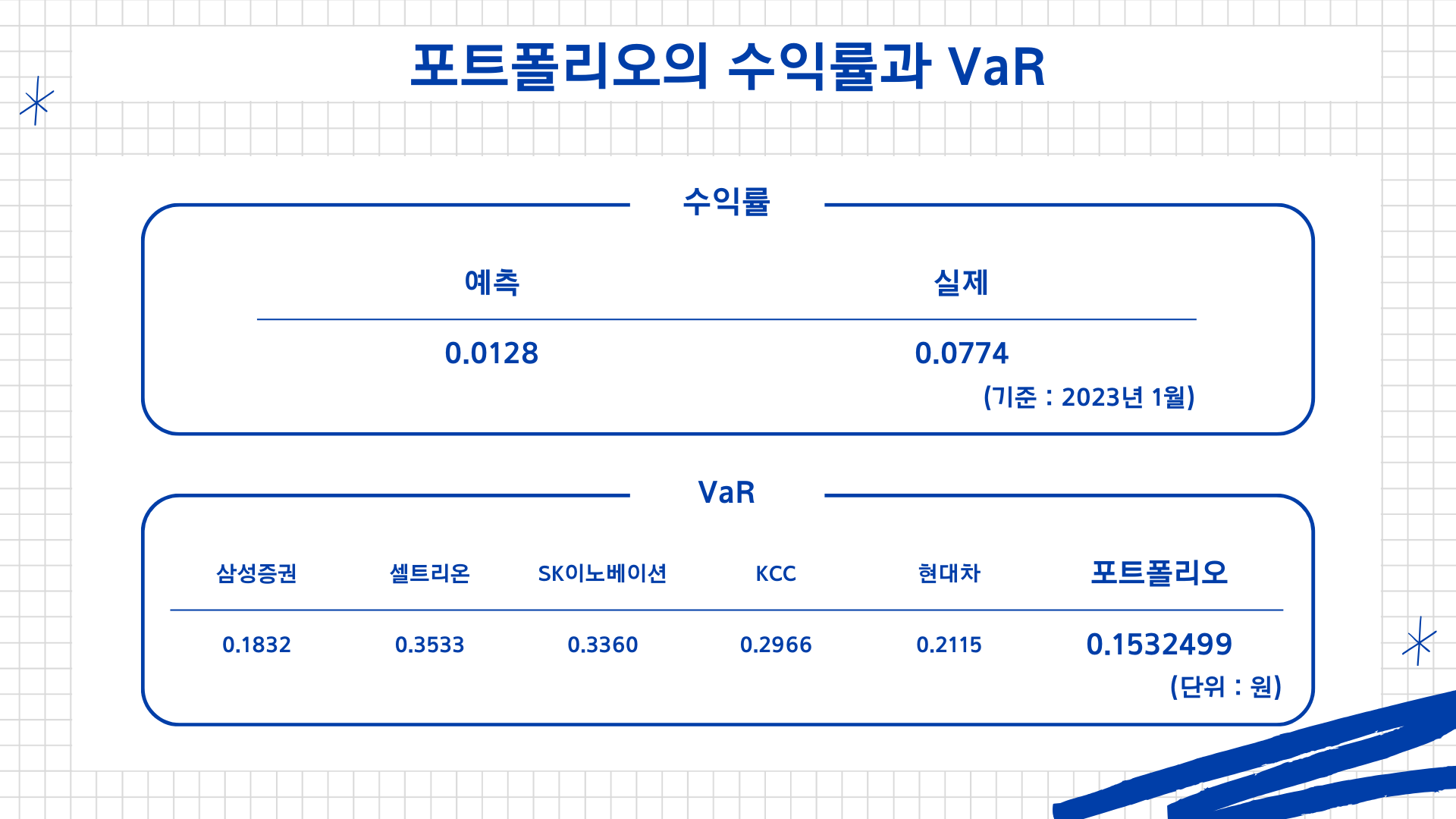
위에서 구한 투자 가중치를 이용해 포트폴리오의 예측 수익률과 VaR는 위와 같다.
VaR 부분을 주의 깊게 보면 포트폴리오의 VaR가 그 어떤 종목의 VaR보다도 낮다는 것을 알 수 있다.
#Conclusion&Limitations


우리 프로젝트의 결론은 다음과 같다.
첫째, 종목의 수익률 예측에 적합한 획일적인 모델은 존재하지 않는다.
둘째, 일부 종목에서는 인과관계가 있는 변수로 만든 VAR 모델보다 AR 모델이 더 적합했던 것처럼 인과관계가 있는 변수가 많은 것과 모델의 설명력은 비례하지 않는다.
셋째, 정확한 수익률 예측보다 추세 예측에 의의를 두었다.
넷째, VaR를 통해 분산 투자를 통해 위험을 낮춘다는 포트폴리오 이론을 확인할 수 있었다.
한계점은 다음과 같다.
첫째, VAR 모델은 매우 단순한 시계열 모델 중 하나로 실제 금융 시장과 많은 차이가 존재할 수 있다.
또한 우리가 선택한 변수 이외에 수익률에 영향을 주는 또다른 변수의 존재 가능성도 배제할 수 없다.
둘째, 적절한 예측 모델을 선정하기 위한 객관적인 지표가 필요하다.
VAR, AR 모델은 예측을 진행할수록 예측한 값을 이용해 예측하는 특성이 있다.
그러다보니 어느 시점부터는 예측값이 무의미해진다.
그래서 우리는 모델별 예측값의 그래프를 통해 예측을 시작한 시점부터 실제 값과 추세가 가장 비슷한 모델을 선택했는데,
적절한 모델을 선택하기 위한 객관적인 지표가 필요하다고 생각하였다.
셋째, RiskMetrics는 다른 VaR 측정 방법에 비해 VaR를 과소 측정하는 경향이 존재한다.
그 이유는 수익률이 표준정규분포를 따른다고 가정하는 RiskMetrics의 특성 때문이다.
실제 수익률은 t-분포에 가깝고, t-분포는 표준정규분포보다 더 두꺼운 꼬리를 갖고있다.
그러다보니 표준정규분포를 가정한 RiskMetrics는 t-분포를 가정한 다른 방법에 비해 VaR를 더 낮게 측정하게 된다.
#프로젝트를마무리하며
정상성의 개념부터 시작해서 AR과 VAR 모델, 인과관계 검정까지 거치면서 시계열을 처음 접하는 조원들이 시계열이 어떤 것인지 알수 있었던 프로젝트였던 것 같다.
이번 프로젝트에서는 머신러닝이나 딥러닝을 사용하지 않았는데, 다음에 또 시계열 프로젝트를 진행하게 되면 사용해보고 싶은 생각이 든다.
서로 처음만나고 약 5주라는 시간동안 누구보다 열심히 참여해주고 따라와준 수정이, 나현이, 준우, 형석이에게 정말로 고마워어어어어어어어엉:)
오늘은 여기까지.
'Project' 카테고리의 다른 글
| [PJ01-03] Value at Risk 측정 및 종목별 가중치 설정 (0) | 2024.02.17 |
|---|---|
| [PJ01-02] VAR 모델링을 통한 예측과 실젯값과의 비교 (1) | 2024.02.08 |
| [PJ01-01] 정상성 검정과 인과관계 검정 with R (0) | 2024.02.01 |

