13. Value at Risk(3)
지난 포스팅에서는 또다른 위험지표인 Expected Shortfall에 대해 알아보았다.
이번 포스팅부터는 Value at Risk(VaR)을 측정하는 다양한 방법에 대해 알아보려고 한다.
기본적으로 다양한 방법이란 수익률과 변동성에 서로다른 시계열 모델을 적용하는 것을 의미한다.
이번 포스팅에서는 다양한 방법 중 하나인 RiskMetrics에 대해 알아본다.
RiskMetrics는 J.P. Morgan에서 개발한 VaR 측정 방법이다.
그 방법은 다음과 같다.
| Def 13.1. (RiskMetrics) $\$1$에 대한 손실을 $x_t^*$라고 할때 RiskMetrics는 $$ x_t^* = \varepsilon_t,$$ $$\sigma_t^2 = a \varepsilon_{t-1}^2 + (1-a) \sigma_{t-1}^2, \tag{1}$$ $ \text{where}~\varepsilon_t = \sigma_t z_t,~z_t \overset{iid}{\sim}N(0,1)$임을 가정한다. |
즉 RiskMetrics는 손실을 ARMA(0,0), 변동성이 IGARCH(1,1)을 따른다고 가정한 방법이다.
IGARCH(1,1) 모델로 서술된 조건부 분산 $\sigma_t^2$은 다음과 같은 결과를 얻게된다.

위의 결과를 이용하면 다음과 같은 성질을 얻을 수 있다.
| Proposition 13.2. $x_{t+k}^*$를 시점 $(t+k)$에서의 손실이라고 할 때, $k=1,2,\cdots$에 대하여 $$ x_{t+k}^* | I_t \sim N(0, \sigma_t^2 [1]),$$ $\text{where}~\sigma_t^2[1]$은 식 (1)을 이용한 1-step forecast. |
위 성질은 중요하므로 간단하게 증명을 살펴보자.
proof of Proposition 13.2.
우리는 위에서 얻은 IGARCH(1,1) 모델의 결과로 다음 식을 알고있다.
$$ \sigma_{t+k}^2 = a [\sigma_{t+k-1}^2 z_{t+k-1}^2 + (1-a)\sigma_{t+k-2}^2 z_{t+k-2}^2 + \cdots].$$
위 식은 $\sigma_{t+k}^2$가 $\sigma_{t+k-1}, \sigma_{t+k-2},\cdots$와 $ z_{t+k-1}, z_{t+k-2}, \cdots$의 함수라는 것을 의미한다.
마찬가지로 $\sigma_{t+k-1}^2$도 $\sigma_{t+k-2}, \sigma_{t+k-3},\cdots$와 $ z_{t+k-2}, z_{t+k-3}, \cdots$의 함수라는 것 또한 알 수 있다.
위 과정을 계속해나가면 결과적으로 $\sigma_{t+k}^2$는 $ z_{t+k-1}, z_{t+k-2}, \cdots$만의 함수로 나타나고 $\sigma_{t+k}$와 $\z_{t+k}$가 독립임을 알 수 있다.
그렇다면 $x_{t+k}^* = \sigma_{t+k} z_{t+k}$의 평균과 분산을 다음과 같이 구할 수 있다.


분산을 구하는 과정을 더 전개하면 다음과 같다.
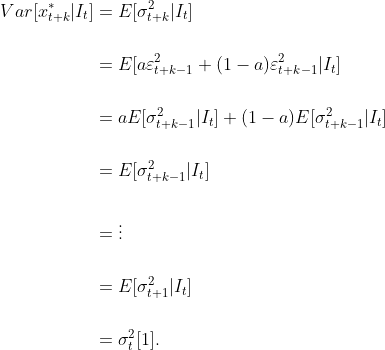
이때 $z_{t+k} \overset{iid}{\sim}N(0,1)$이므로 $x_{t+k}^*|I_t \sim N(0, \sigma_t^2[1])$임을 알 수 있다. $\square$
이제 각 시점에서의 손실에 대한 분포를 구했으므로 향후 우리가 원하는 기간 동안의 손실에 대해 알아보자.
| Proposition 13.3. $x_{t+1 \rightarrow t+s}^*$를 $\$1$에 대한 $s$-기간 손실이라고 할 때, RiskMetrics는 $$ x_{t+1 \rightarrow t+s}^* \sim N(0, s \sigma_t^2[1]),$$ 임을 나타낸다. |
위 성질에 대한 증명도 살펴보자.
proof of Proposition 13.3.
우리는 로그 수익률을 이용하므로 $ x_{t+1 \rightarrow t+s}^* = x_{t+1}^* + \cdots + x_{t+s}^*$임을 알 수 있고 이를 통해 $E[ x_{t+1 \rightarrow t+s}^* |I_t] = 0$임을 쉽게 보일 수 있다.
또한 $E[x_{t+k}^*|I_t]=0$, $z_{t+k}$와 $\sigma_{t+k}$는 독립, $x_{t+k}^* = \sigma_{t+k} z_{t+k}$임을 이용하면 서로 다른 $m,n$에 대하여

임을 알 수 있고 이를 통해
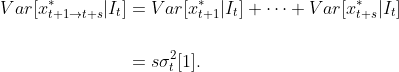
임을 알 수 있다. $\square$
위 결과를 종합하면 RiskMetrics를 이용하여 VaR와 ES를 구하는 식은 다음과 같다.
$$ VaR_{1-p}^* = z_{1-p} \sqrt{s \sigma_t^2[1]}$$
$$ ES_{1-p}^* = \frac{\phi(z_{1-p})}{p} \sqrt{s \sigma_t^2[1]}$$
오늘은 VaR와 ES를 측정하는 방법 중 하나인 RiskMetrics에 대해 알아보았다.
실제 필드에서 VaR나 ES를 구할 때 RiskMetrics를 가장 많이 사용한다고 한다.
가장 큰 이유는 최종 결론에서 본 것과 같이 매우 간단하고 이해하기 쉽기 때문이다.
하지만 다음과 같은 단점 또한 존재한다.
(1) 정규성 가정이 VaR을 과소평가 할 수 있다. 경험적으로 수익률 분포는 정규분포보다 두꺼운 꼬릴 가진 분포를 띄는 경향이 있기 때문이다.
(2) 손익의 평균이 0이라고 가정한 것이 타당하지 않을 수 있다.
(3) IGARCH(1,1) 모델이 변동성을 표현하기에 부적절할 수 있다.
위와 같은 단점들을 극복하는 방법들에 대해 다음 포스팅에서 더 알아보자.
오늘은 여기까지.